Linear Diophantine Equation

from the name it's clear that it's an equation of degree 1.
ax+by=g.c.d.(a,b)=d ...(I)
is also an linear Diophantine equation.According to Bézout's identity if equation number (I) holds true.i.e. gcd(a,b)=d satisfies then, there should be an integer solution of this equation.It's true for more than two variables as well.
Lets take an example
14x+35y=7
As, gcd(14,35)=7 hence Bézout's identity holds true.
Now we can verify it.(x,y)::(-2,1) is an integer solution set of this equation.
Fermat's Last Theorem
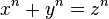
If n=2 this equation becomes x^2+y^2=z^2 nothing but Pythagorian triplets of (x,y,z). Infinite numbers of solution exist.
But if n>=3 no solution exists. This is known as Fermat's Last Theorem
Pell's Equation

this equation is known as Pell's equation, Where n is a non square integer.Trivially x=1, y=0 is one of the solutions of this equation.But there could be other values ,till infinity, as well.
Now by squaring we can write
(x^2-ny^2)^2=1
=>(x^2+ny^2)^2-n(2xy)^2=1
=>(2x^2+1)^2-n(2xy)^2=1 [If x^2-ny^2=-1]...(I)
or, (2x^2-1)^2-n(2xy)^2=1[If x^2-ny^2=1]....(II)
(I) and (II) are also another form of Pell's equation.
Erdős–Straus conjecture

For n>=2, 4/n can be expressed as the summation of three fractional numbers.
Wacław Franciszek Sierpiński generalized this equation and stated that,
for any positive k there exists a number N such that, for all n ≥ N, there exists a solution in positive integers to k/n =1/x+1/y+1/z
one of my problem is 3x+20y=42.find solutions
ReplyDeleteInfinite solution exists.
ReplyDeleteExplanation (1)
(x,y)=>(6,6),(2,9),(14,0),(18,-3),(22,-6)...
Explanation (II)
Equation of a straight line
Infinite solution possible.