 Descartes' theorem (1964)
Descartes' theorem (1964)If four mutually tangent circles have curvature ki (for i = 1,...,4), (ki=1/ri, Where ri is radius)
| (1) |
| (2) |
Other criteria may favor one solution over the other in any given problem.
Special case
If one of the three circles is replaced by a straight line, then one ki, say k3, is zero and drops out of equation (1). Equation (2) then becomes much simpler:
| (3) |
If three circles of radius 1 touches one another then find the radius of the circle which can be inserted within these circles, touching all the three.[CAT]
Solution:
k4=3+2root(3)[positive for inscribed circle] therefore radius=1/[3+2root(3)]=[2-root(3)]/root(3)
PS:One can use conventional method too.


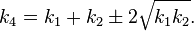
No comments:
Post a Comment